Appearance
H3_COVERAGE_GEODESIC
Returns a list of H3 cells that minimally cover the supplied GEOGRAPHY shape at the given target resolution.
See also:
Syntax
sql
H3_COVERAGE_GEODESIC(<shape>, <target_resolution>, <partial>, <interpolate> = false)Arguments
<shape>: AGEOGRAPHYobject.<target_resolution>: An integer between 0 and 15 (inclusive) specifying the H3 resolution of the returned cells.<partial>: If false, returns only cells that are fully contained within the shape. If true, returns cells that overlap with the shape.<interpolate>: If false, uses a more accurate but slower geodesic algorithm. If true, uses a faster, interpolated algorithm that may produce incorrect results in extremely rare cases.
Returns
Returns a single-column table with the schema:
sql
h3_coverage_geodesic BIGINTEach row represents a cell covering the supplied shape.
Unlike the official H3 reference implementation, this version follows geodesic lines on the sphere.
It uses a spherical approximation, so edges are arcs rather than straight lines.
If partial is true, a cell is included in the result set if its boundary intersects the input shape.
Providing a resolution outside the valid range results in an error.
No rows are returned if the input geography is NULL or EMPTY.
An error is raised if the function attempts to return more than 200,000 rows.
The definition of "inside a polygon" is the same as in ST_Contains, ST_Intersects, and other geography functions: it always refers to the smaller side. This means a single polygon cannot be larger than one hemisphere.
If multiple components are overlapping in a collection, H3_COVERAGE_GEODESIC may return duplicate cells.
Note
The function requires the configuration parameter enable_full_funcscan to be set to true.
Comparison: Geodesic vs. Interpolated vs. Linear Paths
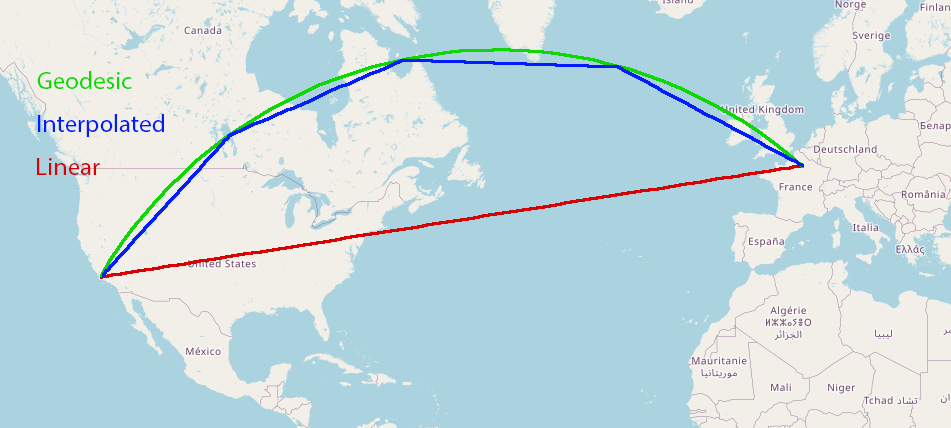
Figure: Comparison of arc representations between San Francisco and Paris
- Geodesic (green): Follows the true curvature of the Earth.
- Interpolated (blue): Approximates the geodesic using multiple straight segments.
- Linear (red): Connects endpoints using a straight line in planar space. Used in
h3_coveage
Geodesic vs. Interpolated Coverage
Yellowbrick supports two modes for computing geographic coverage with the h3_coverage_geodesic function:
Geodesic mode (default): Produces the most accurate representation by treating arcs as great-circle segments on the ellipsoidal Earth surface.
Interpolated mode: Approximates geodesic arcs using a sequence of straight segments. This method closely follows the geodesic path with minimal loss in precision, while offering significantly improved performance.
In internal benchmarks, interpolated mode delivers up to 10× faster execution with negligible accuracy impact for most workloads.
Best Practices
- Use interpolated mode for analytics workloads where performance is critical and small deviations from true arcs are acceptable.
- Use geodesic mode when precise spatial fidelity is required, such as in regulatory, legal, or navigation scenarios.
For accelerated geographic joins this behavior is controlled via the geospatial_join_rewrite_use_geodesic configuration variable.
Example
sql
Create TABLE geo (geo geography);
INSERT INTO geo VALUES ('POINT(0 1)'), ('POLYGON((0 0, 1 0, 1 1, 0 1, 0 0))') , ('LINESTRING(0 0, 0 1, 1 1)');
SELECT * from geo left join h3_coverage_geodesic(geo.geo, 4, true) partial on true left join h3_coverage_geodesic(geo.geo, 4, false) total on total = partial;
-- geo | partial | total
-- --------------------------------+--------------------+--------------------
-- POINT(0 1) | 8475433ffffffff |
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 8475413ffffffff |
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 8475417ffffffff |
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 847541bffffffff |
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 8475433ffffffff |
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 847543bffffffff |
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 847548dffffffff |
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 84754a9ffffffff |
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 84754c1ffffffff |
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 84754c3ffffffff |
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 84754c5ffffffff |
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 84754c7ffffffff |
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 84754cdffffffff |
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 84754e1ffffffff | 84754e1ffffffff
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 84754e3ffffffff |
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 84754e5ffffffff |
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 84754e7ffffffff |
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 84754e9ffffffff | 84754e9ffffffff
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 84754ebffffffff | 84754ebffffffff
-- POLYGON((0 0,1 0,1 1,0 1,0 0)) | 84754edffffffff | 84754edffffffff
-- LINESTRING(0 0,0 1,1 1) | 8475413ffffffff |
-- LINESTRING(0 0,0 1,1 1) | 8475417ffffffff |
-- LINESTRING(0 0,0 1,1 1) | 847541bffffffff |
-- LINESTRING(0 0,0 1,1 1) | 8475433ffffffff |
-- LINESTRING(0 0,0 1,1 1) | 847543bffffffff |
-- LINESTRING(0 0,0 1,1 1) | 84754a9ffffffff |
-- LINESTRING(0 0,0 1,1 1) | 84754e5ffffffff |
-- LINESTRING(0 0,0 1,1 1) | 84754e7ffffffff |